Contents
Target Outcome
To compare two geometries (meshes) and determine how consistent they are with one another. Ultimately, the end goal is to generate a colorized mesh that, based on its color, indicates to what degree the particular mesh resembles another.
Prerequisites
Infrastructure
MeshLab. MeshLab is an open source, portable, and extensible system for the processing and editing of unstructured 3D triangular meshes (GPL license, see http://meshlab.sourceforge.net/).
Previous Protocols
For more information, see:
Comparing Two Geometries
Hausdorff Distances
Hausdorff distance is defined as the "maximum distance of a set to the nearest point in another set." [Rote] This distance essentially "measures the extent to which each point of a 'model' set lies near some point of an 'image' set, and vice versa." [Huttenlocher] With that being said, the Hausdorff distance can be used to "determine the degree of resemblance when two objects are superimposed on one another." [Huttenlocher] With two geometries, the Hausdorff distance is dependent upon which geometries is selected as the target geometry and which is selected as the sampled geometry. For analysis, the following process should be done with the two geometries as both the target and sampled geometries (mesh) to ensure an accurate comparison. In other words, the process should be repeated and the geometries (meshes) should be switched.
Process
- Load both .stl geometry files into Meshlab.
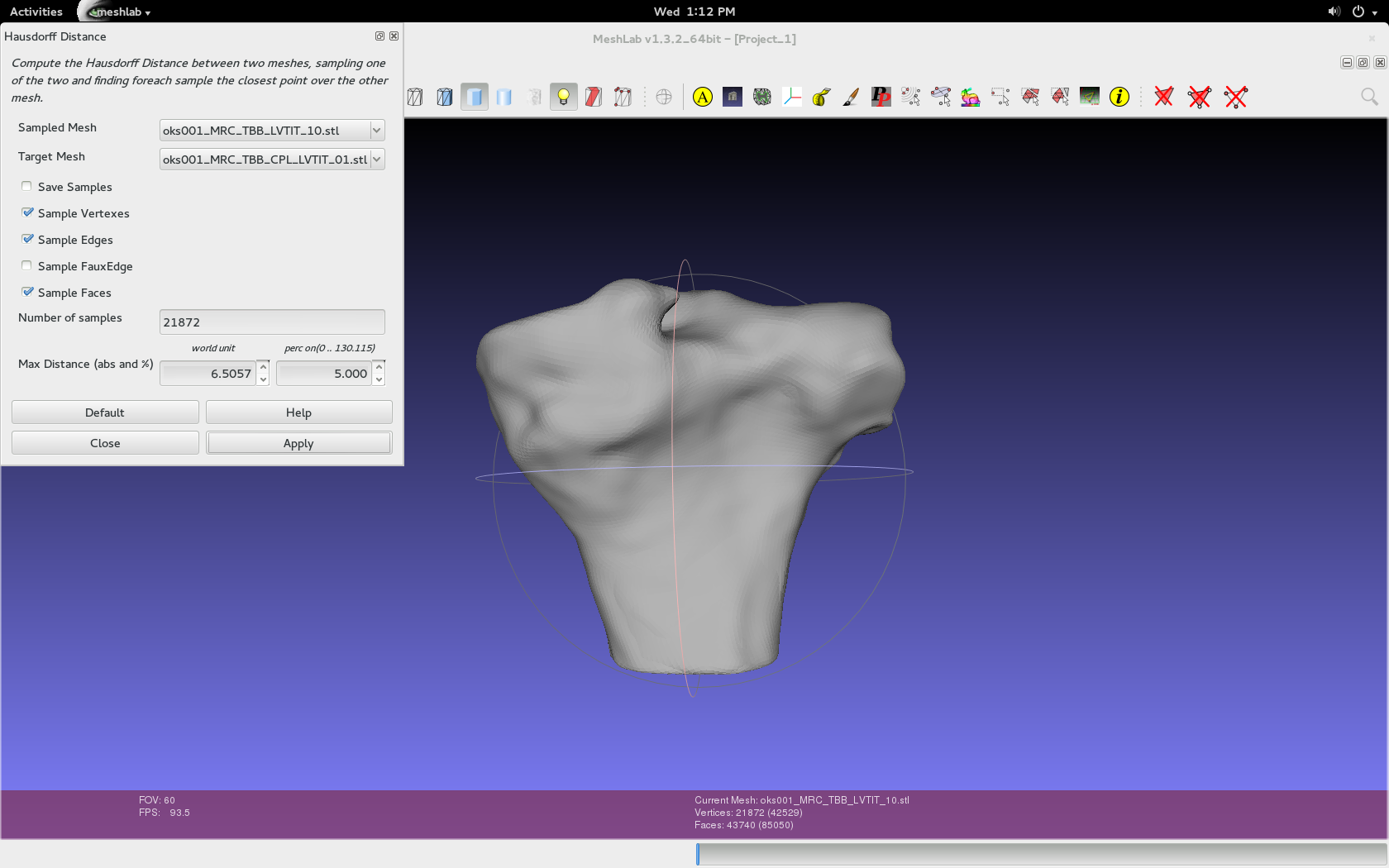
Filters > Sampling > Hausdorff Distance. Use the default values specific to the imported geometries, as seen in the image below. Either can be the target or sampled mesh, but make sure to repeat and switch.
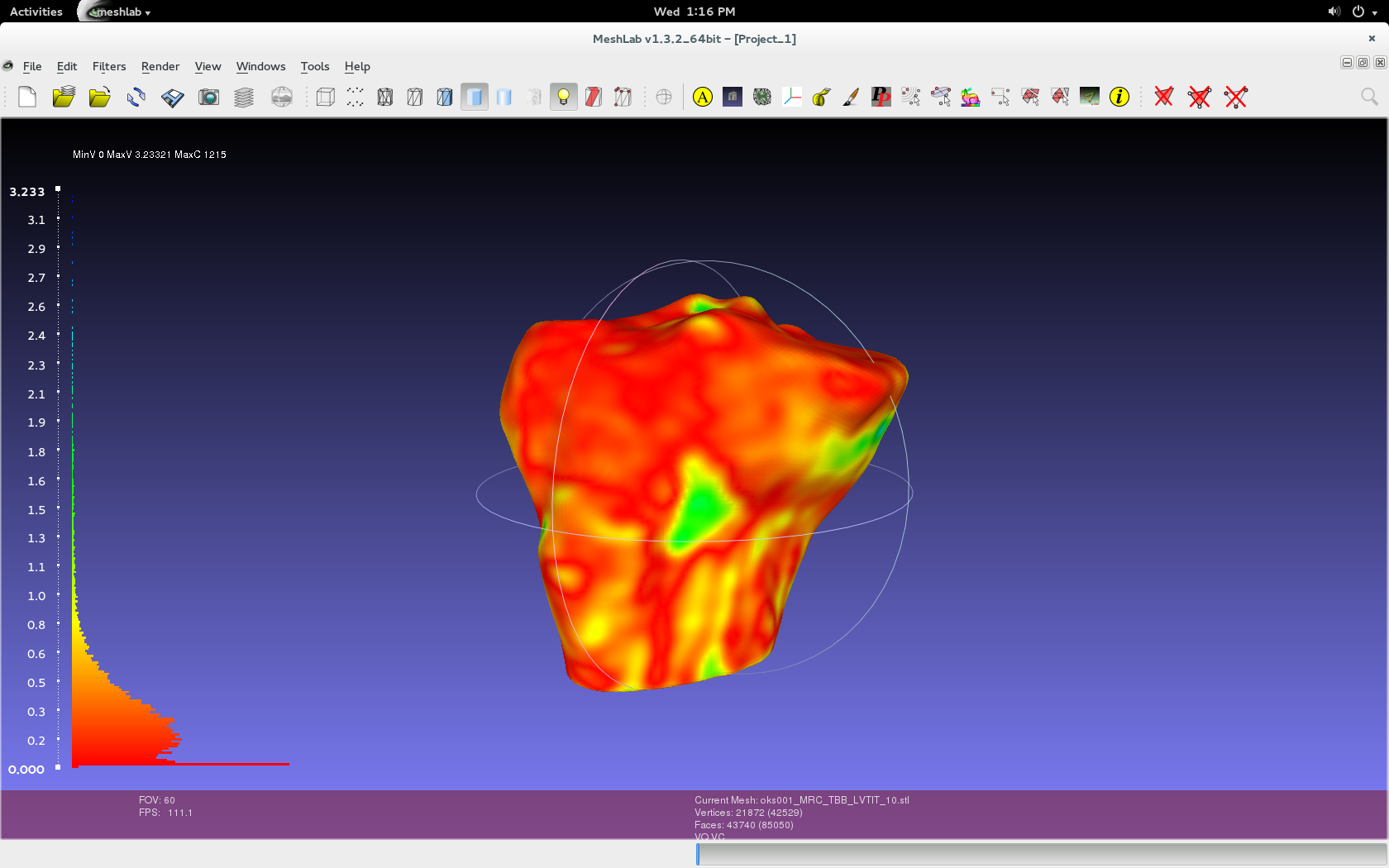
Filters > Color Creation and Processing > Colorize by Vertex Quality. Use the default values specific to the imported geometries, as shown in below image.
- Play with show layer dialogue in order to see just the layer (geometry/mesh) that was colorized (one will have color, other won't). Red will indicate less of an error relative to the blue, which indicates large inconsistency.
Render > Show Vert Quality Histogram
Explanation
Automating Meshlab
For Smoothing
For Comparison
References
G. Rote (1991). Computing the minimum Hausdorff distance between two point sets on a line under translation. Information Processing Letters, v. 38, pp. 123-127.
Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing Images Using the Hausdorff Distance. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1993 September; Vol. 15, No. 9, pg 850. PDF Link