Specifications
Description
The zero force reference lengths (or "slack length") of the ligamentous knee structures have been shown to be important contributors to overall joint mechanics. As they are difficult to measure, ligament slack lengths are a commonly targeted parameter during optimization of specimen-specific joint level kinetic-kinematic response. Regardless of the level of refinement in the modeling approach, whether continuum or spring based, a parameter based representation facilitates these iterative studies.
Ideally, this behavior could be defined either along the ligament line of action or locally within a given element. While the local mesh coordinate frames could be used to approximate a ligament's line of action (if hexahedral elements are used), it would also be convenient to incorporate ligament wrapping, without needing to remesh to reflect this behavior (if possible).
Test Problem
The test problem will be developed using the following:
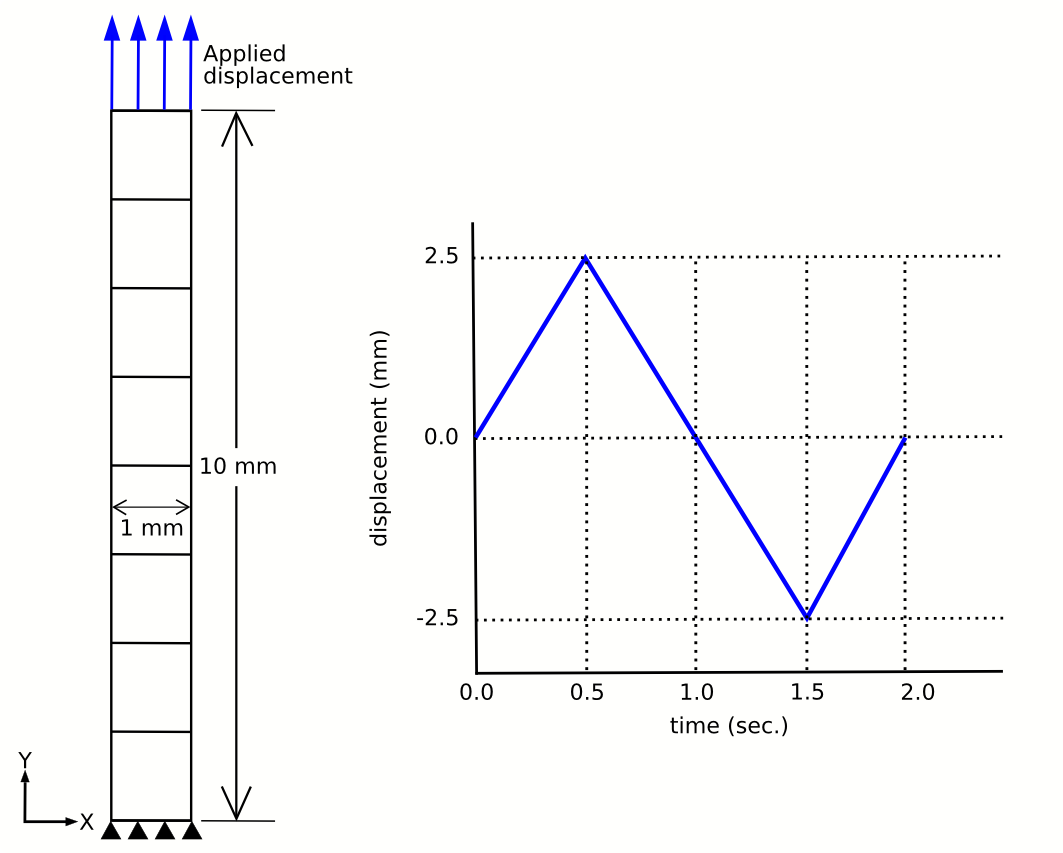
- Geometry/Mesh: a 1 by 1 by 10 mm mesh with fiber direction defined along the 10 mm length.
- Boundary Conditions: a ramp displacement profile (+/- 2.5 mm load-unload) applied to one end of the mesh along the fiber direction (see figure below). The other end is fixed.
- Material Model: a fiber based model, e.g. transversely isotropic Mooney-Rivlin.
Sensitivity: fiber direction in situ strain values ranging -0.2 to +0.2, in 0.1 increments.
- Output: force-displacement response of the loaded end of the mesh.
- For application in Open Knee(s) simulations, implementation in both implicit static and implicit dynamic analyses.
Estimated Completion
April, 2014
Progress
An algorithm for enforcing a user-defined fiber stretch has been implemented in FEBio2. The implementation is based on the paper by Weiss et. al [1] and uses an iterative method for enforcing the prescribed in-situ fiber stretch while maintaining stress equilibrium. The current implementation only works with transversely isotropic Mooney-Rivlin materials but can easily be expanded to other constitutive models. The examples below show the current capabilities.
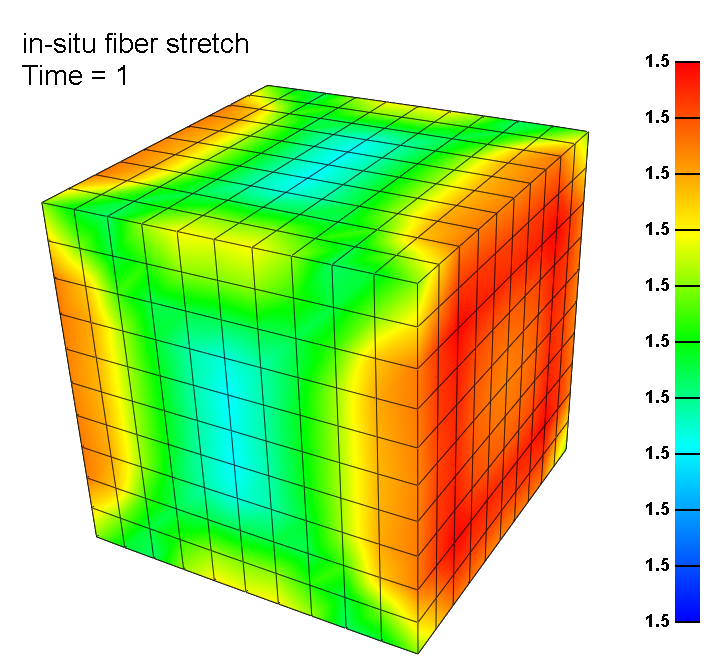
Example 1: A constant in-situ fiber stretch of 50% was enforced on a cubical block. The example shows that a constant fiber strain can be achieved while maintaining stress equilibrium.
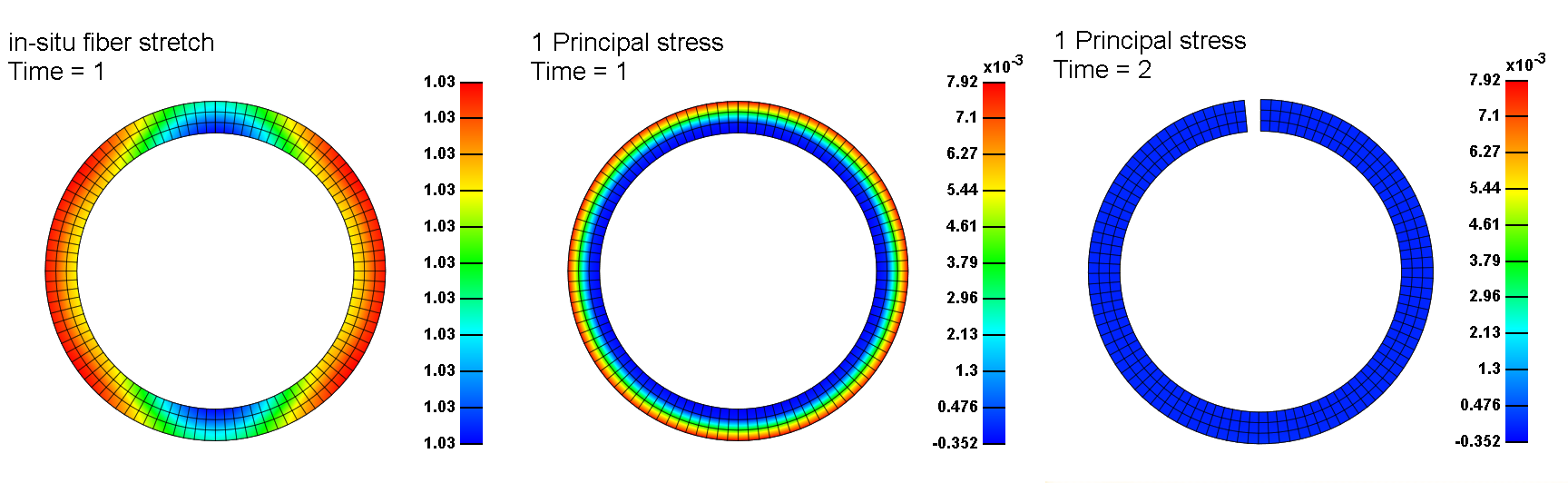
Example 2: A constant in-situ fiber stretch of 3% is prescribed on a cylindrical geometry with the fibers oriented circumferentially (left panel). The first principal stress is shown in the middle panel. A radial cut is introduced which relieves the stresses and introducing the opening angle.
[1] Weiss J.A., Gardiner J.C., Ellis B.J., Lujan T.J., Phatak N.S., Three-dimensional finite element modeling of ligaments: Technical aspects, Medical Engineering & Physics 27 (2005) 845-861
Test problem implementation in FEBio
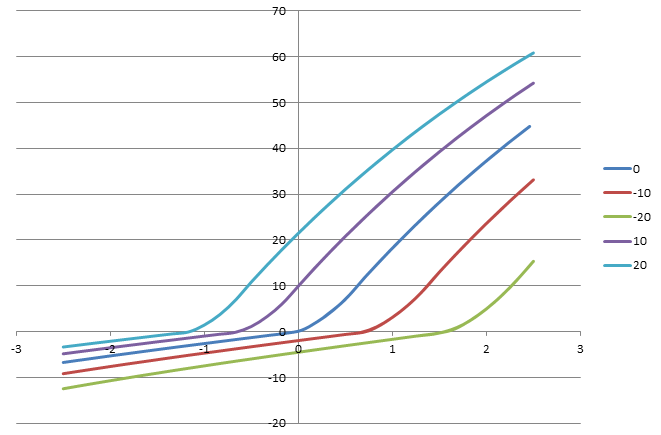
The implementation of the in-situ stretch was tested with the proposed test problem. The geometry was created in PreView and the analysis was done as a two-step analysis. In the first step, the in-situ strain is enforced using the algorithm described above. In the next step a saw-tooth prescribed displacement was applied on the free end of the beam. The model uses a trans-iso Mooney-Rivlin material and the stress-displacement is shown below for different levels of in-situ stretch.
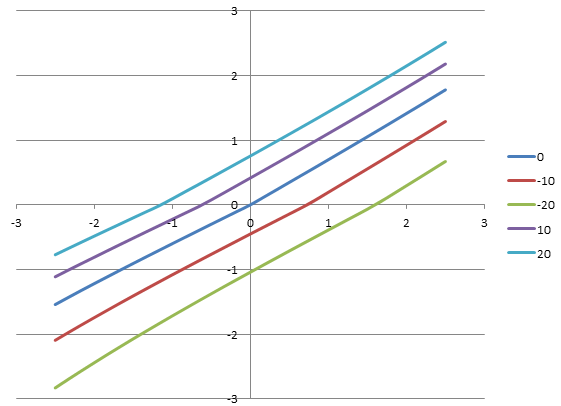
-- aerdemir 2013-12-20 09:35:05 It seems like the material model is not tension only. If it is, I would suspect to see zero force/stress based on in situ strain level. Also, for the in situ strain case of 0.1 (if nominal) zero length of the object will be around 9.09 mm. For -1 mm displacement from reference length (10 mm), I would suspect the force/stress be less then zero as the nominal strain will be approximately -0.01. According to the plot above, the force/stress drops to zero at a displacement of ~ -1.75 mm. Any insight on this will be helpful.
-- belgiansteve 2014-02-23 18:52:07 I've found a problem with the initial test runs. The in-situ strain was being enforced during the entire analysis instead of during the first step. This fix changed the results significantly. I've also confirmed that for the case 0 in the figure the result is now identical to the regular trans-iso MR material in FEBio (which was not the case either in the previous runs).
Another test problem
A repeat of test 1 but with different material parameters. The parameters are: c1 = 4.36, c2=0, c3=2.4, c4=30.6, c5=323, k=100, lambda=1.055.
Three-Dimensional Ligament Problem
Solution of a three-dimensional ligament problem will be reproduced (see Weiss et al., 2005).
-- aerdemir 2014-02-26 20:17:27 Steve, do you mind summarizing this problem with links to the manuscript in here?
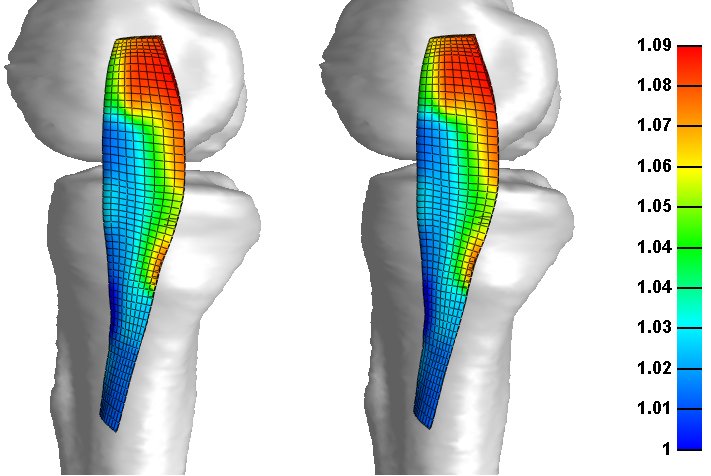
In this problem we match the experimentally measured in-situ stretch for the MCL. The measured in-situ stretches were input as the target stretches for the pre-strain trans-iso Mooney-Rivlin material. Using the augmented Lagrangian method as described above the fiber stretches were determined to match the target stretches. The geometry and material parameters were taken from the original Nike3D model (described in the paper). The target stretches were actually the final stretches from the Nike3D model (since I couldn't find the corresponding Topaz file). The results produce by FEBio matched the Nike3D results excellently. (see figure below, (left) NIKE3D result, (right) FEBio).
Cardiovascular Test Problem for Generalization
A more challenging test problem, relevant to cardiovascular research, can be found in work by Cardamone et al. (2009). In this study a mixture model of an arterial segment (see Figure 1 of Cardamone et al., 2009), with an axial pre-stretch and a circumferential residual stress, was explored. Generalization of in situ strain feature of FEBio to such problems will likely extend its userbase, who may be interested in cardiovascular simulations. Model parameters are provided in Table 1 of Cardamone et al. (2009).
-- belgiansteve 2014-06-04 16:41:00 I realized that the current implementation only applied the in-situ strain to the deviatoric component of the Cauchy-stress in an uncoupled formulation. It is unclear whether this is the correct approach for uncoupled materials. Although this issue needs to be addressed, it was decided to reimplement the in-situ strain algorithm in a coupled formulation first, before solving the problem for uncoupled materials. To date, the following progress was made:
- Implementation of a new material which allows the user to define a pre-strain deformation gradient for any of the materials in FEBio.
- Extending the previous implementation to allow the user to define the pre-strain deformation gradient at each element of the mesh.