PDSystemSolver Class Reference

#include <IpPDSystemSolver.hpp>

Inheritance diagram for PDSystemSolver:

Detailed Description

Pure Primal Dual System Solver Base Class.

This is the base class for all derived Primal-Dual System Solver Types.

Here, we understand the primal-dual system as the following linear system:

$\left[\begin{array}{cccccccc} W & 0 & J_c^T & J_d^T & -P^x_L & P^x_U & 0 & 0 \\ 0 & 0 & 0 & -I & 0 & 0 & -P_L^d & P_U^d \\ J_c & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ J_d & -I & 0 & 0 & 0 & 0 & 0 & 0\\ Z_L(P_L^x)^T & 0 & 0 & 0 & Sl^x_L & 0 & 0 & 0\\ -Z_U(P_U^x)^T & 0 & 0 & 0 & 0 & Sl^x_U & 0 & 0\\ 0 & V_L(P_L^d)^T & 0 & 0 & 0 & 0 & Sl^s_L & 0 \\ 0 & -V_U(P_U^d)^T & 0 & 0 & 0 & 0 & 0 & Sl^s_U \\ \end{array}\right] \left(\begin{array}{c} sol_x\\ sol_s\\ sol_c\\ sol_d\\ sol^z_L\\ sol^z_U\\ sol^v_L\\ sol^v_U \end{array}\right) = \left(\begin{array}{c} rhs_x\\ rhs_s\\ rhs_c\\ rhs_d\\ rhs^z_L\\ rhs^z_U\\ rhs^v_L\\ rhs^v_U \end{array}\right)$

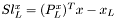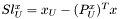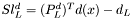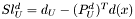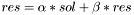Here, $Sl^x_L = (P^x_L)^T x - x_L$ , $Sl^x_U = x_U - (P^x_U)^T x$ , $Sl^d_L = (P^d_L)^T d(x) - d_L$ , $Sl^d_U = d_U - (P^d_U)^T d(x)$ . The results returned to the caller is $res = \alpha * sol + \beta * res$ .

The solution of this linear system (in order to compute the search direction of the algorthim) usually requires a considerable amount of computation time. Therefore, it is important to tailor the solution of this system to the characteristics of the problem. The purpose of this base class is to provide a generic interface to the algorithm that it can use whenever it requires a solution of the above system. Particular implementation can then be written to provide the methods defined here.

It is implicitly assumed here, that the upper left 2 by 2 block is possibly modified (implicitly or explicitly) so that its projection onto the null space of the overall constraint Jacobian $\left[\begin{array}{cc}J_c & 0\\J_d & -I\end{array}\right]$ is positive definite. This is necessary to guarantee certain descent properties of the resulting search direction. For example, in the full space implementation, a multiple of the identity might be added to the upper left 2 by 2 block.

Note that the Solve method might be called several times for different right hand sides, but with identical data. Therefore, if possible, an implemetation of PDSystem should check whether the incoming data has changed, and not redo factorization etc. unless necessary.

Public Member Functions

virtual bool InitializeImpl (const OptionsList &options, const std::string &prefix)=0

overloaded from AlgorithmStrategyObject

virtual bool Solve (Number alpha, Number beta, const IteratesVector &rhs, IteratesVector &res, bool allow_inexact=false, bool improve_solution=false)=0

Solve the primal dual system, given one right hand side.

/Destructor

PDSystemSolver ()

Default Constructor.

virtual ~PDSystemSolver ()

Default destructor.

Constructor & Destructor Documentation

PDSystemSolver ( ) [inline]

Default Constructor.

virtual ~PDSystemSolver ( ) [inline, virtual]

Default destructor.

Member Function Documentation

virtual bool InitializeImpl	(	const OptionsList &	options,
		const std::string &	prefix
	)			`[pure virtual]`

overloaded from AlgorithmStrategyObject

Implements AlgorithmStrategyObject.

Implemented in PDFullSpaceSolver.

virtual bool Solve	(	Number	alpha,
		Number	beta,
		const IteratesVector &	rhs,
		IteratesVector &	res,
		bool	allow_inexact = `false`,
		bool	improve_solution = `false`
	)			`[pure virtual]`

Solve the primal dual system, given one right hand side.

If the flag allow_inexact is set to true, it is not necessary to solve the system to best accuracy; for example, we don't want iterative refinement during the computation of the second order correction. On the other hand, if improve_solution is true, the solution given in res should be improved (here beta has to be zero, and res is assume to be the solution for the system using rhs, without the factor alpha...). THe return value is false, if a solution could not be computed (for example, when the Hessian regularization parameter becomes too large.)

Implemented in PDFullSpaceSolver.

The documentation for this class was generated from the following file:

IpPDSystemSolver.hpp


Public Member Functions
virtual bool	InitializeImpl (const OptionsList &options, const std::string &prefix)=0
	overloaded from AlgorithmStrategyObject
virtual bool	Solve (Number alpha, Number beta, const IteratesVector &rhs, IteratesVector &res, bool allow_inexact=false, bool improve_solution=false)=0
	Solve the primal dual system, given one right hand side.
/Destructor
	PDSystemSolver ()
	Default Constructor.
virtual	~PDSystemSolver ()
	Default destructor.